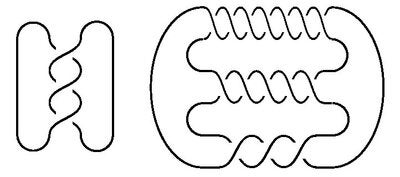
In mathematics, knots are more than simply scrunched up bundles of cords. To a mathematician, a knot is an embedding of a circle into 3-dimensional space which is a fancy way of saying it is a closed loop which may cross over itself when we project it onto a plane (e.g. let it fall to the floor). Two knots are the same mathematically if one can be smoothly transformed into the other without breaking the loop or allowing it to pass through itself. The figure below shows a few knots, some simple and others complicated. There are only four different knots that can be drawn using four or fewer crossings (try it!), but as the number of crossings grows, the number of different knots grows exponentially and quickly becomes difficult to differentiate. There are more than 1.7 million knots with 16 crossings, making it nearly impossible to compare these large knots by hand.
Topologists care about knots because they are related to a class of spaces called manifolds. A 2-manifold (or surface) is a space that locally looks like a 2-dimensional (Euclidean) plain but may have some global topology. For example, the rubber skin of a beach ball is a 2-manifold: you can cut a small piece of it out and flatten it out on the surface of a table, but the flattened surface still exists within the context of the larger object. The same is true for the rubber surface of an inner tube (a torus). So, these two spaces locally look the same, even though they are globally different. A 3-manifold is similar, but now the piece looks locally like a 3-dimensional space.
Knots are a rich source of 3-manifolds. For example, if we remove the points of a knot from the 3-dimensional space its embedded in, what’s left will be a 3-manifold, called the complement of the knot. Different knots produce different 3-manifolds.
How can we tell the difference between knots and understand properties of the 3-manifolds they are related to? These questions have been at the heart of Robert and Ann Canary Professor Jake Rasmussen’s work who has discovered a way to take concepts from symplectic geometry and apply them to knot theory.
Before we can understand how this works, we must understand how knots are differentiated. Knot theorists use something called invariants to help determine if two knots are different. An invariant is a value that will always be the same for any two knots that are mathematically identical; however, it is important to note that this value may also be the same for knots that are not mathematically identical. A simple invariant would be to count the minimal number of crossings in a diagram of the knot. A knot with 6 crossings is obviously not the same as a knot with 7 crossings, but two knots with 6 crossings are not necessarily the same either.
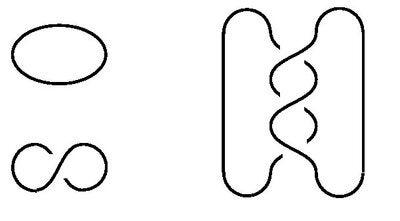
A more complicated invariant is the Alexander polynomial, which was discovered in 1923 by J. W. Alexander. To each knot, it assigns a polynomial with integer coefficients. The Alexander polynomial can be defined using the methods of algebraic topology to define an invariant of the complement of the knot. The Alexander polynomial is a much stronger invariant than the crossing number, but there are still many different knots with the same Alexander polynomial; for example, the knot on the right of Figure 1 has the same Alexander polynomial as the unknot (a knot with zero crossings).
The invariants Rasmussen studies are defined in a similar way to the Alexander Polynomial but utilize concepts from symplectic geometry and topological quantum field theories to define invariants of the complement of the knot. One of these invariants, the knot Floer homology, can be used to recover the Alexander polynomial, but is more powerful at distinguishing knots. For example, there is no other knot with the same knot Floer homology as the unknot. Surprisingly, this property can be used to show that the knot complement itself is a perfect invariant of the knot: two knots with the same complements must themselves be the same.
The knot Floer homology is just one of many examples of how surprising mathematics can be and how advancements in one mathematical field can lead to advancements in another. Rasmussen continues to study the Floer homology of knots and 3-manifolds and is currently working on developing new applications for this method, supported by his Robert and Ann Canary endowed professorship.