
In 1991, physicists studying string theory made a strange discovery that shook up the field of mathematics as we knew it. Using some experimental techniques to predict curve counts in six-dimensional space, they achieved a result that indicated a strong relationship between two very different geometric worlds.
At first, the result was hard for many mathematicians to take seriously. Up to that point, no tool in mathematics had been capable of doing what the physicists had achieved.
Later, when mathematicians were able to confirm the predictions, many fields of mathematical research exploded with possibilities, in some cases spawning brand new areas of study. Questions at the center of that 1991 discovery continue to inspire mathematicians and physicists today.
Professor Felix Janda, who joined the faculty at University of Illinois Urbana-Champaign earlier in fall 2023, is one such mathematician. The work he is doing right now could shake up the dynamics of the field once again.
To understand what impact his research could have, it’s worth considering the historical context surrounding it.
A curious link
Since the 1980s, scientists have been using string theory to explain the existence of subatomic particles such as quarks, electrons, and neutrinos. In string theory, these particles are made of tiny, vibrating strings.
Over time, physicists began to understand that, to account for things like gravitational forces and quantum mechanics, those tiny, vibrating strings must exist in 10 different dimensions—or spaces with unique physical properties.
The observable world comprises four dimensions. So what is going on in those extra six dimensions? How do we define them? These questions fueled a large body of scientific research for several decades.

One thing we know about the extra dimensions is that they must take the shape of a Calabi-Yau threefold; an example of this shape is a quintic threefold. We know this partly because the mathematical fields of algebraic geometry and topology gave us tools we needed to examine and define the extra dimensions.
Algebraic geometry allows us to translate properties of a given space into polynomial equations. Polynomial equations can be graphed so that we can literally study their shape. When polynomials contain complex numbers, they can result in intricate shapes known as “complex manifolds,” or spaces with complex structures.
But not all types of spaces can be defined using complex geometry. For instance, “phase space,” which can be thought of a complete accounting of all possible position and momentum variables in a physical system, is commonly defined by principles of “symplectic geometry.”
For many years, complex and symplectic geometries didn’t seem to have much to do with each other; for one thing, they account for wildly different types of spaces. Complex geometry is quite rigid, whereas symplectic geometry—a tool that, among other things, helps humans define motion—allows much more variance.
One result of that groundbreaking 1991 discovery was the revelation that these two geometric spaces—which had once been deemed so different they had to be studied separately—actually held “mirror symmetries.”
Mirror symmetry is a term used to describe a very specific relationship between geometries. Through the theory of mirror symmetry, one can relate complex structures of one space to symplectic structures in a very different “mirror” space.
For mathematicians, the impact of that revelation was huge: the ability to relate the two geometries suddenly gave researchers on either side of the mirror a whole new faction of tools they might use to study problems in their respective fields.
The problem with curves
The mathematical knowledge available to understand complex and symplectic geometries, and a common language to describe that knowledge, expanded further over the last thirty years. But significant challenges to curve-counting problems remained.
For one, when those physicists1 were making predictions about curves in 1991, they were only accounting for specific types of curves—those with algebraic curves of genus zero. Higher genus curves, which produce more complicated geometric objects, are significantly more challenging for mathematicians and physicists to count.
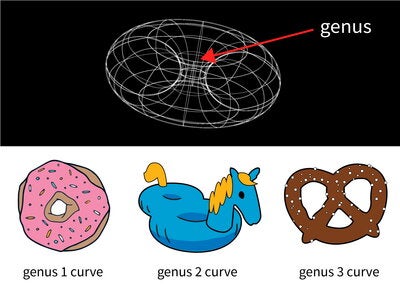
Over time, theoretical physicists developed heuristics to help them grapple with higher genus curves; these methods have been used to predict curve counts on quintic threefolds of up to genus 64.
However, advancement on the mathematical front has been more restricted. This is partly because, broadly speaking, physicists’ methods help them make predictions about curve counts; mathematicians’ work to confirm those predictions often requires a different set of tools. For many years, the tools geometers had at their disposal were not always suitable for tackling curve-counting problems.
It took more than a decade, but mathematicians eventually proved physicists’ genus zero and genus 1 curve predictions. When it came to higher genus curve counts, progress stalled.
Until Felix Janda came up with a new idea.
Creating the log GLSM
Janda, an algebraic geometer, is interested in moduli spaces of curves. Moduli spaces give mathematicians a way to learn about distinct objects—usually geometric objects—in a universal context.
Another way to think of moduli spaces is this: Imagine biologists who are studying the social behaviors of a particular species of animal. Should those biologists choose to study the animals one at a time, they will likely make interesting observations about that species, but those observations may not have a discernible pattern. If they studied those same animals in a group setting, patterns would likely to emerge, giving the biologists important insights about how the species interacts with its environment.
Moduli spaces work like the latter method of observation, allowing mathematicians to zoom out on a given subject and notice patterns. Moduli spaces can be vast, and they are often rife with opportunities to establish connections between different areas of mathematics.
While collaborating with fellow researchers on a study of two specific algebraic objects on the moduli space of curves, Janda found inspiration for a technique that could be applied to new curve-counting problems.
Prominent curve-counting theories include Gromov-Witten theory, Fan-Jarvis-Ruan-Witten (FJRW) theory, quasimap theory, and the gauged sigma linear model (GLSM). Janda’s work traverses each of these theories and finds hidden links between them.
Before Janda, researchers had already worked out how to relate some of these theories to GLSM, which in physics is central to computations of curve counts on the quintic threefold. Many hoped that this would lead to new computations. But, as Janda explains, there was still a missing piece of the puzzle.
“In a nutshell, the technical problem with [using] GLSM in math is that it is based on “non-compact spaces;” in other words, spaces that go off to infinity in some direction,” says Janda.
Logarithmic geometry, a branch of geometry first developed to study problems in number theory, offered a possible solution, as it can be quite useful for studying non-compact spaces. Using his expertise in curve-counting theories and his observations of curve moduli, Janda collaborated with other geometers to create the logarithmic gauged linear sigma model, or log GLSM.
Janda says that “in some sense, log GLSM is an application of logarithmic geometry to GLSM, and thus, curve counts.”
According to his peers, the log GLSM is a powerful new framework that could resolve some of the most challenging curve-counting problems. While Janda is still working to further develop the full framework for the log GLSM, it has already been employed to solve several longstanding problems in Gromov-Witten theory. It has the potential to answer many more.
For Janda, the foundational work for log GLSM also presents opportunities to find new mathematical relationships.
“One aspect of my area of study that I particularly enjoy is its interplay between geometry and computations,” says Janda. “Simple geometric facts can translate into profound relations between curve counts, while patterns in curve counts can uncover geometric structures that had not been observed before.”
Janda recently received an NSF CAREER grant that will support his work in completing the geometric foundations for log GLSM.
The applicability of Janda’s methods in other fields is not yet known, but given the steady interchange of ideas between mathematics and physics that preceded him, it’s possible that such applications exist.
As for what new discoveries await researchers armed with a fully realized log GLSM, only time will tell.
1. The physicists referred to here are Philip Candelas, Xenia C. De la Ossa, Paul S. Green, and Linda Parkes.↩